改变世界的10个数学方程式

精选最重要，最漂亮的数学方程式

> Picture by Antoine Dautry on Unsplash

多年来，数学一直在帮助我们更好地理解世界，同样，我们也利用世界来更好地理解数学。 数学学科以人类的经验和几千年来发展起来的共同思想为基础。 从某种意义上说，通过使用数学，我们能够解释这个世界上出现的更多现象和联系，因此，一些新的数学发现改变了世界。

在本文中，我将展示10个最重要和最美丽的数学方程式。 本文基于Ian Stewart撰写的"追求未知：改变世界的17个方程"一书。

1.毕达哥拉斯定理（毕达哥拉斯，公元前530年）

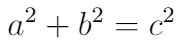
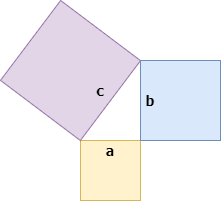
> Example triangle

勾股定理是此处列出的十个定理中最古老的定理，已有近2500年的历史！ 该定理说明了直角三角形的三个边之间的欧几里得几何学的基本关系。 它指出边为斜边的正方形的面积（与直角相对的边）等于其他两个边上的正方形的面积之和。 该定理可以写成与边a，b和c的长度相关的方程，通常称为"毕达哥拉斯方程"（如上所述），其中c代表斜边的长度，而a和b是三角形的边的长度。 其他两个方面。

2.对数（John Napier，1610）

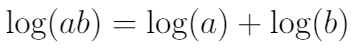
上面的对数方程立即显示出其最重要的应用之一：它能够将乘法转化为加法。 几年前，当必须手动完成所有计算时，此属性的确导致了更快的计算。

当然，这不是它的唯一用途。 众所周知，对数是一个逆运算，因为它可以消除指数效应。 此外，对数是表示大数的一种非常方便的方式（数字的基数10以对数表示该数字的位数：log（98765）≈4.99）。

3.微积分（牛顿，1668年）

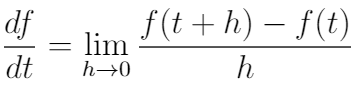
上式是微积分中导数的定义。 导数测量数量变化的速率。 从基本演算到多元演算，导数都有许多重要的应用。

4.正态分布（C.F.高斯，1810年）

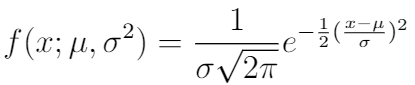
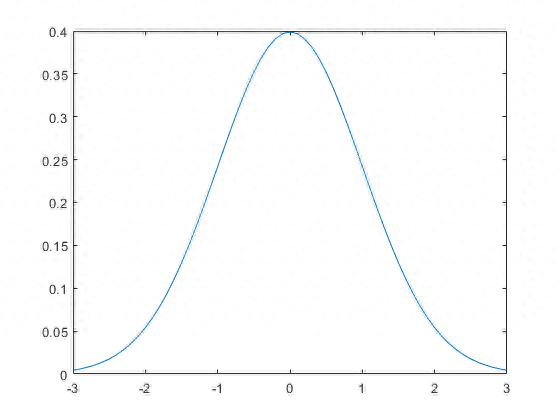
> Standard normal N(0,1) distribution

正态分布是统计中最重要的概率分布。 之所以如此，是因为这种分布适合许多自然现象。 这种分布也称为高斯分布，以C.F. 高斯 从图片中可以看出，它是对称分布。 正态分布取决于两个参数：平均值μ和标准偏差σ。 这两个参数完全定义了正态分布的形状和概率。 平均值定义正态分布的峰的位置，标准偏差定义宽度。 同样，分布两端的极小值也不太可能。

正态分布经常用于诸如IQ分数测量误差和高度分布之类的应用中。

5.负一的平方根（R.笛卡尔，17世纪）

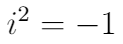
该方程式是复数的基础，可以将其写成实数乘以虚数单位i。 复数用于实际应用中，例如电路。

6.欧拉公式（欧拉，1748年）

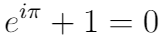
该方程式被认为是数学之美的典范，因为它表明了数学中最基本的数字之间的深刻联系。 1990年，《数学情报家》（The Mathematical Intelligencer）对读者进行了一次调查，称欧拉的身份为“数学上最美丽的定理”。在由Physics World于2004年进行的另一次读者调查中，欧拉的身份与麦克斯韦方程组并列为“有史以来最伟大的方程式”。

7.麦克斯韦方程（J.C.麦克斯韦，1865年）

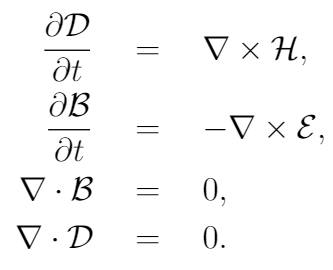
麦克斯韦方程组是一组耦合的偏微分方程组，与洛伦兹力定律一起构成了经典电磁学，经典光学和电路的基础。 这些方程式描述了电荷，电流和磁场变化如何产生电场和磁场。

麦克斯韦方程的一个重要结果是，它们证明了波动的电场和磁场如何在真空中以恒定速度（c）传播。

8.相对论（爱因斯坦，1905年）

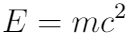
这个经典方程式表明，具有质量的任何事物都具有相等的能量，反之亦然（质量能量等效）。 等效能量（E）可以计算为质量（m）乘以光速（c）的平方。 由于光速在日常单位中是大量的，因此该公式意味着即使静止不动的日常物体也具有非常大的内在能量。

9.信息论（C. Shannon，1949）

给定的方程式用于信息熵，这是信息论中与任何随机变量关联的数量。 该熵是无序的量度。 在这里，它测量消息的信息内容（书籍，JPEG图片或可以象征性表示的任何内容）。 消息的熵表示在不丢失其某些内容的情况下可以压缩该消息的数量的下限。

由Shannon引入的这种熵测度启动了信息的数学研究，其结果对于当今我们如何通过网络进行通信至关重要。

10. Black-Scholes方程（F. Black and M. Scholes，1990）

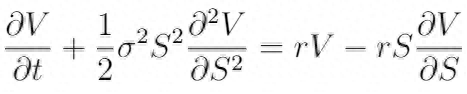
Black-Scholes等式描述了金融专家和交易员如何查找衍生工具的价格，衍生工具是基于某些基础资产的金融产品。 衍生工具是现代金融体系的重要组成部分。

该方程式背后的关键见解是，在无摩擦市场的模型假设下，人们可以通过以正确的方式买卖基础资产来完全对冲期权，从而"消除风险"。 反过来，这种套期保值意味着该期权只有一个正确的价格，这是布莱克-舒尔斯公式所返回的。

等式的左侧由"时间衰减"项，导数值相对于时间的变化以及涉及第二空间导数的项，导数值相对于基础值的凸度组成。 右侧是从衍生工具的多头头寸和空头头寸无风险的收益。

结论

在本文中，我们看到了10个改变世界的数学方程式。 当然，还有许多其他的数学发现对世界产生了巨大的影响。 数学在不断发展，我们的社会也在不断发展。

(本文翻译自Maurizio Sluijmers的文章《10 Mathematical Equations That Changed The World》，参考：https://medium.com/swlh/10-mathematical-equations-that-changed-the-world-a3264f79927d)